前幾天我們看了編碼理論的介紹，準備工作已經結束，今天我們可以正式介紹「編碼密碼系統」的架構！

系統架構

場景：Bob 想傳送訊息給 Alice

鑰匙生成

Alice 準備一個線性編碼 C ，他是一個接收訊息長度為 k 編碼長度為 n 並且可以更正 t 個錯誤的編碼。這個 C 可以是 Hamming code ，也可以是 RS code ，構造上並無限制。我們用函數 D 來代表解碼演算法。

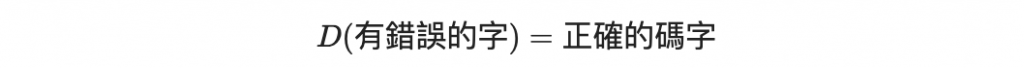
我們用字母 G 來代表 C 的生成矩陣。

生成一個 k 乘 k 大小的可逆矩陣 S 與一個 n 乘 n 大小的排列矩陣 P （見下文），這些是被當作私鑰。

所謂的排列矩陣就是對單位矩陣的「行」進行排列的矩陣，舉例如

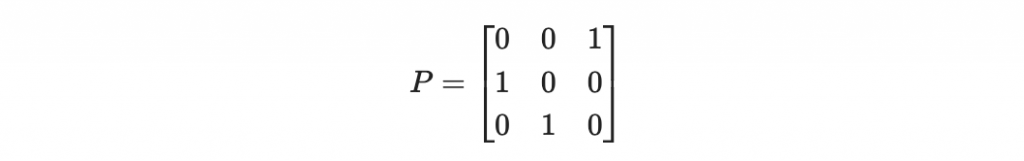
就是一個 把第一行調換到第三行、第二行調換到第一行、第三行調換到第二行 的排列矩陣。

計算混淆過後的生成矩陣

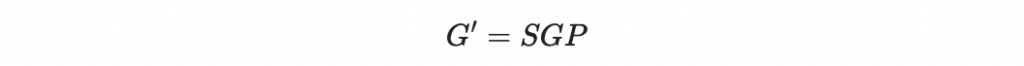
這個 G' 生成了一個新的編碼系統 C'，而 C' 又是 C 的某種線性變換加上排列，這代表說，C' 的結構與 C 的結構是很類似，但是因為有前後的 S 與 P 所以 C' 看起來很隨機。（是不是很像雙極構造法，見 Day10）

而針對 C 的解碼演算法 D 並不能直接用在 C' 的解碼上，原因是乘在前面的排列矩陣 P 會把相關資料打亂。若 C 是用 Hamming code ，則檢查碼的位置被打亂；若 C 是用 RS code ，則多項式插值的相關資料被打亂。

你若是想要研究 C' 的更正演算法，你就需要先猜到那個私鑰裡的 P 是什麼，這有 n! 個可能。編碼密碼系統的安全性就來自於「看似隨機的編碼系統無法輕易解碼的困難性」 即使你知道這個看似隨機的編碼背後的架構（如 Hamming 或 RS），也難以直接使用相同的解碼演算法 D 來更正 C' 的錯誤。

公鑰為

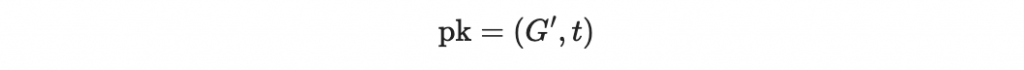
其中 t 是編碼 C 的錯誤更正能力。

私鑰為

加密

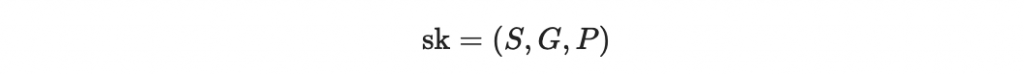
Bob 選擇要加密的訊息 m ，其長度為 k

計算密文

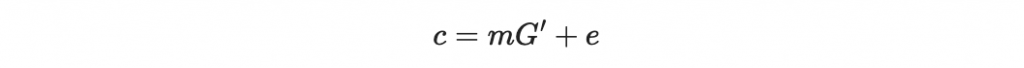
其中 e 是最多 t 個非零元素的錯誤向量。於是 c 就是一個 C' 中的碼字 mG' 加上幾個錯誤位元 e 。

將密文傳送給 Alice。

如前所述，儘管 C' 的結構與 C 相似，但解碼演算法 D 無法直接應用於 C'。因此，即使攻擊者獲得了密文 c，且理論上 C' 可以更正其中的錯誤 e，也因為 C' 是經過混淆的，攻擊者無法透過解碼來還原訊息 m。

當然，如果攻擊者非常勤奮，他也可以暴力嘗試所有 n! 種排列矩陣 P，如果碰巧猜對了，則有可能解出訊息。（這種運氣拿去買樂透不好嗎？）

解碼

Alice 拿到密文後根據私鑰裡的 P ，他可以計算

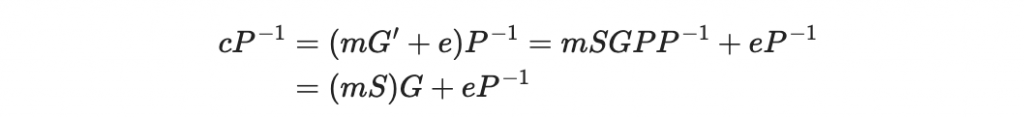
注意到 P^(-1) 就是將排列反著做，所以還是一個排列矩陣。因此 eP^(-1) 仍然是一個最多 t 個非零元素的錯誤向量。

這個 cP^(-1) 就可以解釋為 訊息 (mS) 經過在編碼系統 C 下的編碼 加上最多 t 個錯誤的錯誤向量 eP^(-1) 。

此時 Alice 就可以表演解碼演算法 D ，從 cP^(-1) 中解出 (mS) 。

最後的最後， Alice 使用私鑰裡面的可逆矩陣 S ，計算

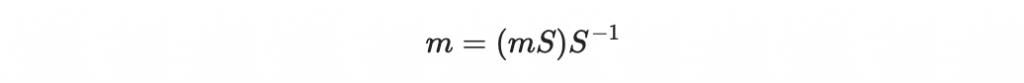
這樣她就能成功恢復出原始訊息 m。

SageMath 實作

我們使用 RS code 當作構造中的編碼系統 C

參數與鑰匙生成

決定編碼的參數：

# Parameters of code

q = 677
n = 10
k = 4
R = quotient(ZZ, q*ZZ)

# 生成 n 個不重複且非零的插值點
alphas = []
while len(alphas) < n:
    elem = R.random_element()
    if elem not in alphas and elem != 0:
        alphas.append(elem)
print(f"插值點:")
print(alphas)

# Outputs:
# 插值點:
# [513, 278, 49, 129, 336, 443, 347, 554, 562, 165]

編碼生成矩陣 G

# 編碼的生成矩陣 G: k x n
G = Matrix(
    R,
    [
        [alphas[i]^j for i in range(n)]
        for j in range(k)
    ]
)
print("編碼的生成矩陣 G:")
print(G)

# Outputs:
# 編碼的生成矩陣 G:
# [  1   1   1   1   1   1   1   1   1   1]
# [513 278  49 129 336 443 347 554 562 165]
# [493 106 370 393 514 596 580 235 362 145]
# [388 357 528 599  69 675 191 206 344 230]

生成私鑰中的排列矩陣 P

# 生成 n x n 的排列矩陣 P
perm = [i for i in range(1,n+1)]
shuffle(perm)
p = Permutation(perm)
# 使用 permutation.to_matrix() 方法生成排列矩陣
P = p.to_matrix()

print("排列矩陣 P:")
print(P)

# Outputs:
# 排列矩陣 P:
# [0 0 0 0 1 0 0 0 0 0]
# [0 0 0 1 0 0 0 0 0 0]
# [0 0 0 0 0 1 0 0 0 0]
# [0 0 0 0 0 0 0 0 1 0]
# [1 0 0 0 0 0 0 0 0 0]
# [0 0 0 0 0 0 0 1 0 0]
# [0 0 1 0 0 0 0 0 0 0]
# [0 0 0 0 0 0 1 0 0 0]
# [0 1 0 0 0 0 0 0 0 0]
# [0 0 0 0 0 0 0 0 0 1]

生成私鑰中的可逆矩陣 S

# 生成 k x k 的隨機可逆矩陣 S
while True:
    S = random_matrix(R, k, k)
    if S.is_invertible():
        break
print("可逆矩陣 S:")
print(S)

# Outputs: 
# 可逆矩陣 S:
# [135  49 423 619]
# [604 324 109 233]
# [664 155  31   7]
# [517 285 159 270]

計算公鑰

# 生成公開生成矩陣 G_public = S * G * P
G_public = S * G * P
print("公開生成矩陣 G_public:")
print(G_public)

# 設定可更正錯誤量 t
t = (n - k) // 2
print(f"可更正錯誤量 t: {t}")

# 公鑰 pk 包含 G_public 和 t
pk = (G_public, t)

# 私鑰 sk 包含 G, S, P
sk = (G, S, P)

# Outputs:
# 公開生成矩陣 G_public:
# [516 398 233 654  83 469 325 558 522  24]
# [135 360  53 590 214 429 515 118  40 245]
# [107 531 650 118  13 407 481 458 477 525]
# [303 382 159  46 170 586 225 294 177   5]
# 可更正錯誤量 t: 3

加密

def encrypt(pk,message):
    G_public, t = pk

    message = vector(message)

    # 生成錯誤向量 e ，錯誤個數最多為 t 
    error_vector = vector([0 for _ in range(n)])
    # 隨機選擇 t 個錯誤位置
    error_positions = sample([_ for _ in range(n)], t)  # 隨機選擇 t 個位置
    for pos in error_positions:
        error = 0
        while error == 0:
            error = R.random_element()
            
        error_vector[pos] = error

    cipher = message * G_public + error_vector

    return cipher.list()
        
    


message = [R.random_element() for i in range(k)]
print("原始訊息：")
print(message)
cipher = encrypt(pk, message)
print("加密訊息：")
print(cipher)

# Outputs:
# 原始訊息：
# [268, 418, 669, 48]
# 加密訊息：
# [567, 432, 374, 426, 213, 322, 610, 123, 170, 624]

解密

先計算出 cP^(-1)

P_inv = P.transpose() # 因為 P 是排列矩陣，所以 P 的反矩陣就是他的轉置，下一行就檢查
# 檢查 P 和 P_inv 是否真的是互為逆矩陣
print(P*P_inv == identity_matrix(n)) 

received = (vector(cipher) * (P_inv)).list()

# Outputs:
# True

進行演算法 D （見 Day 27）

# decoding process
# after decoding, we get (message * S)

LinearSystem = [] 
for i in range(n):
    LinearSystem.append(
        [alphas[i]^j for j in range(t+k)] + [-received[i] * alphas[i]^j for j in range(t)]
    )

constant_term = []
for i in range(n):
    constant_term.append( [received[i] * alphas[i]^t])

solution = matrix(LinearSystem).solve_right(matrix(constant_term))

N = solution.list()[:t+k]
E = solution.list()[t+k:]

R_poly = PolynomialRing(R, 'X')
messageS = R_poly(N)/R_poly(E+[1])
messageS = (vector((R_poly(messageS)).list()))

print("解碼結束，得到 message * S 為")
print(messageS)

# Outputs:
# 解碼結束，得到 message * S 為
# (121, 555, 445, 651)

# 最後乘上 S^(-1)
decrypted_message = (messageS * S.inverse()).list()
print(decrypted_message)
print(message)
print(decrypted_message == message)


# Outputs:
# [268, 418, 669, 48]
# [268, 418, 669, 48]
# True

Takeaway

• 編碼密碼系統的安全性：McEliece Framework 利用生成矩陣 GG、排列矩陣 PP 和可逆矩陣 SS 的混淆來確保安全，攻擊者難以通過暴力破解還原訊息，因為排列矩陣有 n!n! 種可能。
• 加密與解密過程：加密將訊息經過 G′G′ 和隨機錯誤向量 ee 生成密文，解密則使用私鑰中的 PP 和 SS 還原訊息。
• SageMath 實作：文中展示了如何利用 SageMath 進行公鑰和私鑰的生成，以及加密與解密操作。

ref:
WEGER, Violetta; GASSNER, Niklas; ROSENTHAL, Joachim. A survey on code-based cryptography.